Sort with a neural networkMachine Learning Golf: MultiplicationCan a neural network recognize primes?Find the largest root of a polynomial with a neural networkPrint the Golden RatioTo Vectory! – The Vector Racing Grand PrixSort some apples!Sort a List With Swaps and PopsPlurality Voting with Cellular AutomataSort by shuffling blocksCan a neural network recognize primes?Machine Learning Golf: MultiplicationFind the largest root of a polynomial with a neural networkImplement the Max-Pooling operation from Convolutional Neural Networks
Between while and do in shell script
Brake disc and pads corrosion, do they need replacement?
Did the computer mouse always output relative x/y and not absolute?
How far apart are stars in a binary system?
Feeling of forcing oneself to do something
Is Jupiter still an anomaly?
How to pay less tax on a high salary?
How could pirates reasonably transport dinosaurs in captivity, some of them enormous, across oceans?
Best spot within a human to place redundant heart
Why do cargo airplanes fly fewer cycles then airliners?
Next Shared Totient
What is the purpose of the rules in counterpoint composition?
"Don't invest now because the market is high"
Is the use of ellipsis (...) dismissive or rude?
What is homebrew? Should I use it in normal games?
When did Hebrew start replacing Yiddish?
What movie or fandom is this jewelry from?
Defining strength of Moran's I
hfill doesn't work between minipages
How can I convince my department that I have the academic freedom to select textbooks and use multiple-choice tests in my courses?
Is publishing runnable code instead of pseudo code shunned?
Was playing with both hands ever allowed in chess?
Thoughts on using user stories to define business/platform needs?
Why does std::atomic constructor behave different in C++14 and C++17
Sort with a neural network
Machine Learning Golf: MultiplicationCan a neural network recognize primes?Find the largest root of a polynomial with a neural networkPrint the Golden RatioTo Vectory! – The Vector Racing Grand PrixSort some apples!Sort a List With Swaps and PopsPlurality Voting with Cellular AutomataSort by shuffling blocksCan a neural network recognize primes?Machine Learning Golf: MultiplicationFind the largest root of a polynomial with a neural networkImplement the Max-Pooling operation from Convolutional Neural Networks
.everyoneloves__top-leaderboard:empty,.everyoneloves__mid-leaderboard:empty,.everyoneloves__bot-mid-leaderboard:empty
margin-bottom:0;
$begingroup$
The previous neural net golfing challenges (this and that) inspired me to pose a new challenge:
The challenge
Find the smallest feedforward neural network such that, given any 4-dimensional input vector $(a,b,c,d)$ with integer entries in $[-10,10]$, the network outputs $textrmsort(a,b,c,d)$ with a coordinate-wise error strictly smaller than $0.5$.
Admissibility
For this challenge, a feedforward neural network is defined as a composition of layers. A layer is a function $LcolonmathbfR^ntomathbfR^m$ that is specified by a matrix $AinmathbfR^mtimes n$ of weights, a vector $binmathbfR^m$ of biases, and an activation function $fcolonmathbfRtomathbfR$ that is applied coordinate-wise:
$$ L(x) := f(Ax+b), qquad xinmathbfR^n. $$
Since activation functions can be tuned for any given task, we need to restrict the class of activation functions to keep this challenge interesting. The following activation functions are permitted:
Identity. $f(t)=t$
ReLU. $f(t)=operatornamemax(t,0)$
Softplus. $f(t)=ln(e^t+1)$
Hyperbolic tangent. $f(t)=tanh(t)$
Sigmoid. $f(t)=frace^te^t+1$
Overall, an admissible neural net takes the form $L_kcirc L_k-1circcdots circ L_2circ L_1$ for some $k$, where each layer $L_i$ is specified by weights $A_i$, biases $b_i$, and an activation function $f_i$ from the above list. For example, the following neural net is admissible (while it doesn't satisfy the performance goal of this challenge, it may be a useful gadget):
$$left[beginarraycmin(a,b)\max(a,b)endarrayright]=left[beginarrayrrrr1&-1&-frac12&-frac12\1&-1½½endarrayright]mathrmReLUleft[beginarrayrrfrac12½\-frac12&-frac12\1&-1\-1&1endarrayright]left[beginarrayca\bendarrayright]$$
This example exhibits two layers. Both layers have zero bias. The first layer uses ReLU activation, while the second uses identity activation.
Scoring
Your score is the total number of nonzero weights and biases.
(E.g., the above example has a score of 16 since the bias vectors are zero.)
code-challenge optimization neural-networks
$endgroup$
|
show 6 more comments
$begingroup$
The previous neural net golfing challenges (this and that) inspired me to pose a new challenge:
The challenge
Find the smallest feedforward neural network such that, given any 4-dimensional input vector $(a,b,c,d)$ with integer entries in $[-10,10]$, the network outputs $textrmsort(a,b,c,d)$ with a coordinate-wise error strictly smaller than $0.5$.
Admissibility
For this challenge, a feedforward neural network is defined as a composition of layers. A layer is a function $LcolonmathbfR^ntomathbfR^m$ that is specified by a matrix $AinmathbfR^mtimes n$ of weights, a vector $binmathbfR^m$ of biases, and an activation function $fcolonmathbfRtomathbfR$ that is applied coordinate-wise:
$$ L(x) := f(Ax+b), qquad xinmathbfR^n. $$
Since activation functions can be tuned for any given task, we need to restrict the class of activation functions to keep this challenge interesting. The following activation functions are permitted:
Identity. $f(t)=t$
ReLU. $f(t)=operatornamemax(t,0)$
Softplus. $f(t)=ln(e^t+1)$
Hyperbolic tangent. $f(t)=tanh(t)$
Sigmoid. $f(t)=frace^te^t+1$
Overall, an admissible neural net takes the form $L_kcirc L_k-1circcdots circ L_2circ L_1$ for some $k$, where each layer $L_i$ is specified by weights $A_i$, biases $b_i$, and an activation function $f_i$ from the above list. For example, the following neural net is admissible (while it doesn't satisfy the performance goal of this challenge, it may be a useful gadget):
$$left[beginarraycmin(a,b)\max(a,b)endarrayright]=left[beginarrayrrrr1&-1&-frac12&-frac12\1&-1½½endarrayright]mathrmReLUleft[beginarrayrrfrac12½\-frac12&-frac12\1&-1\-1&1endarrayright]left[beginarrayca\bendarrayright]$$
This example exhibits two layers. Both layers have zero bias. The first layer uses ReLU activation, while the second uses identity activation.
Scoring
Your score is the total number of nonzero weights and biases.
(E.g., the above example has a score of 16 since the bias vectors are zero.)
code-challenge optimization neural-networks
$endgroup$
2
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
1
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
1
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
3
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
1
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16
|
show 6 more comments
$begingroup$
The previous neural net golfing challenges (this and that) inspired me to pose a new challenge:
The challenge
Find the smallest feedforward neural network such that, given any 4-dimensional input vector $(a,b,c,d)$ with integer entries in $[-10,10]$, the network outputs $textrmsort(a,b,c,d)$ with a coordinate-wise error strictly smaller than $0.5$.
Admissibility
For this challenge, a feedforward neural network is defined as a composition of layers. A layer is a function $LcolonmathbfR^ntomathbfR^m$ that is specified by a matrix $AinmathbfR^mtimes n$ of weights, a vector $binmathbfR^m$ of biases, and an activation function $fcolonmathbfRtomathbfR$ that is applied coordinate-wise:
$$ L(x) := f(Ax+b), qquad xinmathbfR^n. $$
Since activation functions can be tuned for any given task, we need to restrict the class of activation functions to keep this challenge interesting. The following activation functions are permitted:
Identity. $f(t)=t$
ReLU. $f(t)=operatornamemax(t,0)$
Softplus. $f(t)=ln(e^t+1)$
Hyperbolic tangent. $f(t)=tanh(t)$
Sigmoid. $f(t)=frace^te^t+1$
Overall, an admissible neural net takes the form $L_kcirc L_k-1circcdots circ L_2circ L_1$ for some $k$, where each layer $L_i$ is specified by weights $A_i$, biases $b_i$, and an activation function $f_i$ from the above list. For example, the following neural net is admissible (while it doesn't satisfy the performance goal of this challenge, it may be a useful gadget):
$$left[beginarraycmin(a,b)\max(a,b)endarrayright]=left[beginarrayrrrr1&-1&-frac12&-frac12\1&-1½½endarrayright]mathrmReLUleft[beginarrayrrfrac12½\-frac12&-frac12\1&-1\-1&1endarrayright]left[beginarrayca\bendarrayright]$$
This example exhibits two layers. Both layers have zero bias. The first layer uses ReLU activation, while the second uses identity activation.
Scoring
Your score is the total number of nonzero weights and biases.
(E.g., the above example has a score of 16 since the bias vectors are zero.)
code-challenge optimization neural-networks
$endgroup$
The previous neural net golfing challenges (this and that) inspired me to pose a new challenge:
The challenge
Find the smallest feedforward neural network such that, given any 4-dimensional input vector $(a,b,c,d)$ with integer entries in $[-10,10]$, the network outputs $textrmsort(a,b,c,d)$ with a coordinate-wise error strictly smaller than $0.5$.
Admissibility
For this challenge, a feedforward neural network is defined as a composition of layers. A layer is a function $LcolonmathbfR^ntomathbfR^m$ that is specified by a matrix $AinmathbfR^mtimes n$ of weights, a vector $binmathbfR^m$ of biases, and an activation function $fcolonmathbfRtomathbfR$ that is applied coordinate-wise:
$$ L(x) := f(Ax+b), qquad xinmathbfR^n. $$
Since activation functions can be tuned for any given task, we need to restrict the class of activation functions to keep this challenge interesting. The following activation functions are permitted:
Identity. $f(t)=t$
ReLU. $f(t)=operatornamemax(t,0)$
Softplus. $f(t)=ln(e^t+1)$
Hyperbolic tangent. $f(t)=tanh(t)$
Sigmoid. $f(t)=frace^te^t+1$
Overall, an admissible neural net takes the form $L_kcirc L_k-1circcdots circ L_2circ L_1$ for some $k$, where each layer $L_i$ is specified by weights $A_i$, biases $b_i$, and an activation function $f_i$ from the above list. For example, the following neural net is admissible (while it doesn't satisfy the performance goal of this challenge, it may be a useful gadget):
$$left[beginarraycmin(a,b)\max(a,b)endarrayright]=left[beginarrayrrrr1&-1&-frac12&-frac12\1&-1½½endarrayright]mathrmReLUleft[beginarrayrrfrac12½\-frac12&-frac12\1&-1\-1&1endarrayright]left[beginarrayca\bendarrayright]$$
This example exhibits two layers. Both layers have zero bias. The first layer uses ReLU activation, while the second uses identity activation.
Scoring
Your score is the total number of nonzero weights and biases.
(E.g., the above example has a score of 16 since the bias vectors are zero.)
code-challenge optimization neural-networks
code-challenge optimization neural-networks
asked Sep 27 at 11:42
Dustin G. MixonDustin G. Mixon
6771 silver badge10 bronze badges
6771 silver badge10 bronze badges
2
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
1
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
1
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
3
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
1
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16
|
show 6 more comments
2
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
1
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
1
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
3
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
1
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16
2
2
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
1
1
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
1
1
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
3
3
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
1
1
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16
|
show 6 more comments
1 Answer
1
active
oldest
votes
$begingroup$
Octave, 96 88 87 84 76 54 50 weights & biases
This 6-layer neural net is essentially a 3-step sorting network built from a very simple min/max network as a component. It is basically the example network from wikipedia as shown below, with a small modification: The first two comparisons are done in parallel. To bypass negative numbers though the ReLU, we just add 100 first, and then subtract 100 again at the end.
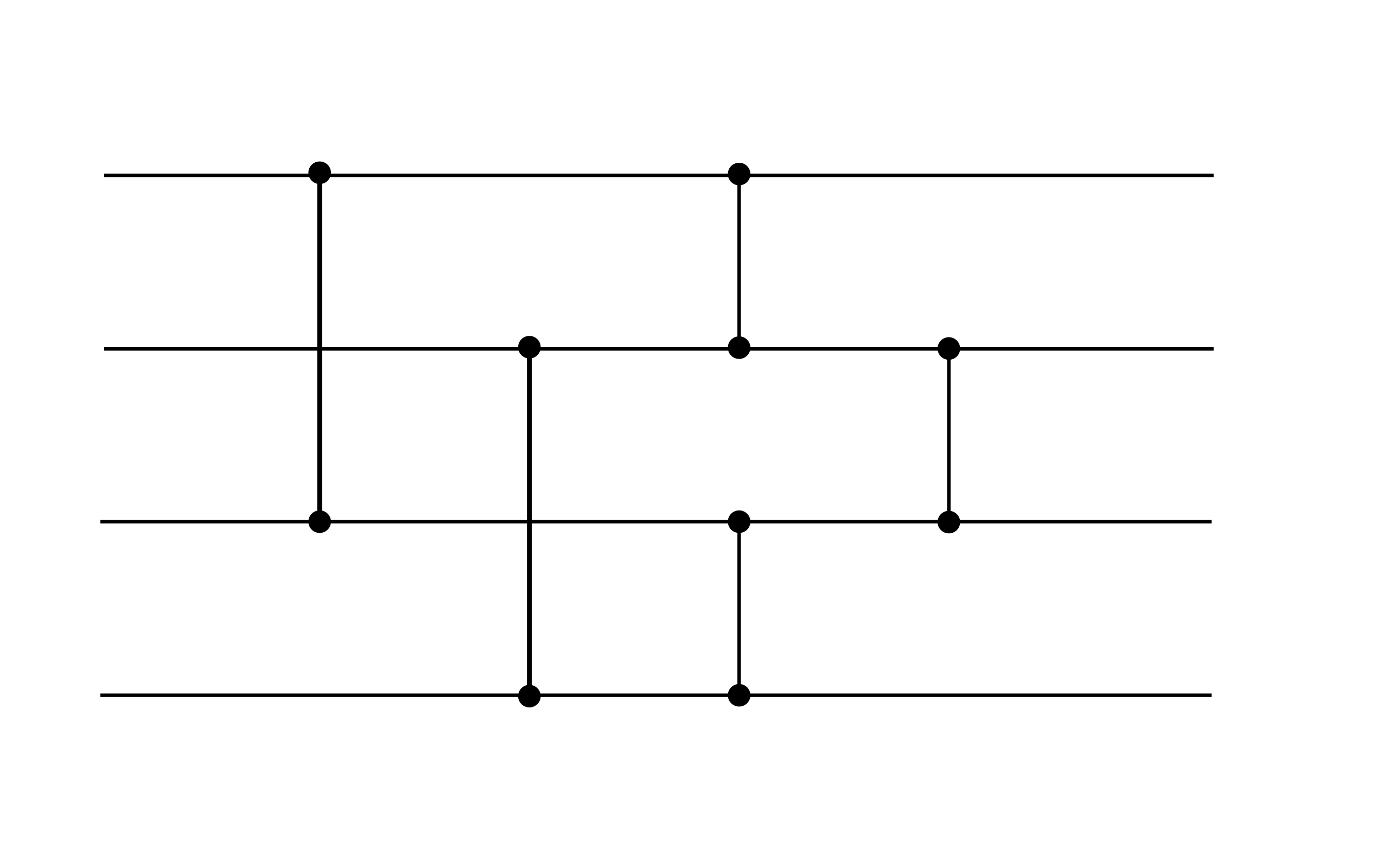
So this should just be considered as a baseline as it is a naive implementation. It does however sort all possible numbers that do not have a too large magnitude perfectly. (We can adjust the range by replacing 100 with another number.)
Try it online!
max/min-component
There is a (considerably less elegant way more elegant now, thanks @xnor!) way to find the minimum and maximum of two numbers using less parameters:
$$beginalign min &= a - ReLU(a-b) \ max &= b + ReLU(a-b) endalign$$
This means we have to use a lot less weights and biases.
Thanks @Joel for pointing out that it is sufficient to make all numbers positive in the first step and reversing it in the last one, which makes -8 weights. Thanks @xnor for pointing out an even shorter max/min method which makes -22 weights! Thanks @DustinG.Mixon for the tip of combining certain matrices which result in another -4 weights!
function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end
Try it online!
$endgroup$
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
$begingroup$
Might you get a shorter min-max gadget with(a - relu(a-b), b + relu(a-b))?
$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
|
show 2 more comments
Your Answer
StackExchange.ifUsing("editor", function ()
StackExchange.using("externalEditor", function ()
StackExchange.using("snippets", function ()
StackExchange.snippets.init();
);
);
, "code-snippets");
StackExchange.ready(function()
var channelOptions =
tags: "".split(" "),
id: "200"
;
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function()
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled)
StackExchange.using("snippets", function()
createEditor();
);
else
createEditor();
);
function createEditor()
StackExchange.prepareEditor(
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: false,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: null,
bindNavPrevention: true,
postfix: "",
imageUploader:
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/4.0/"u003ecc by-sa 4.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
,
onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
);
);
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fcodegolf.stackexchange.com%2fquestions%2f193624%2fsort-with-a-neural-network%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Octave, 96 88 87 84 76 54 50 weights & biases
This 6-layer neural net is essentially a 3-step sorting network built from a very simple min/max network as a component. It is basically the example network from wikipedia as shown below, with a small modification: The first two comparisons are done in parallel. To bypass negative numbers though the ReLU, we just add 100 first, and then subtract 100 again at the end.

So this should just be considered as a baseline as it is a naive implementation. It does however sort all possible numbers that do not have a too large magnitude perfectly. (We can adjust the range by replacing 100 with another number.)
Try it online!
max/min-component
There is a (considerably less elegant way more elegant now, thanks @xnor!) way to find the minimum and maximum of two numbers using less parameters:
$$beginalign min &= a - ReLU(a-b) \ max &= b + ReLU(a-b) endalign$$
This means we have to use a lot less weights and biases.
Thanks @Joel for pointing out that it is sufficient to make all numbers positive in the first step and reversing it in the last one, which makes -8 weights. Thanks @xnor for pointing out an even shorter max/min method which makes -22 weights! Thanks @DustinG.Mixon for the tip of combining certain matrices which result in another -4 weights!
function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end
Try it online!
$endgroup$
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
$begingroup$
Might you get a shorter min-max gadget with(a - relu(a-b), b + relu(a-b))?
$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
|
show 2 more comments
$begingroup$
Octave, 96 88 87 84 76 54 50 weights & biases
This 6-layer neural net is essentially a 3-step sorting network built from a very simple min/max network as a component. It is basically the example network from wikipedia as shown below, with a small modification: The first two comparisons are done in parallel. To bypass negative numbers though the ReLU, we just add 100 first, and then subtract 100 again at the end.

So this should just be considered as a baseline as it is a naive implementation. It does however sort all possible numbers that do not have a too large magnitude perfectly. (We can adjust the range by replacing 100 with another number.)
Try it online!
max/min-component
There is a (considerably less elegant way more elegant now, thanks @xnor!) way to find the minimum and maximum of two numbers using less parameters:
$$beginalign min &= a - ReLU(a-b) \ max &= b + ReLU(a-b) endalign$$
This means we have to use a lot less weights and biases.
Thanks @Joel for pointing out that it is sufficient to make all numbers positive in the first step and reversing it in the last one, which makes -8 weights. Thanks @xnor for pointing out an even shorter max/min method which makes -22 weights! Thanks @DustinG.Mixon for the tip of combining certain matrices which result in another -4 weights!
function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end
Try it online!
$endgroup$
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
$begingroup$
Might you get a shorter min-max gadget with(a - relu(a-b), b + relu(a-b))?
$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
|
show 2 more comments
$begingroup$
Octave, 96 88 87 84 76 54 50 weights & biases
This 6-layer neural net is essentially a 3-step sorting network built from a very simple min/max network as a component. It is basically the example network from wikipedia as shown below, with a small modification: The first two comparisons are done in parallel. To bypass negative numbers though the ReLU, we just add 100 first, and then subtract 100 again at the end.

So this should just be considered as a baseline as it is a naive implementation. It does however sort all possible numbers that do not have a too large magnitude perfectly. (We can adjust the range by replacing 100 with another number.)
Try it online!
max/min-component
There is a (considerably less elegant way more elegant now, thanks @xnor!) way to find the minimum and maximum of two numbers using less parameters:
$$beginalign min &= a - ReLU(a-b) \ max &= b + ReLU(a-b) endalign$$
This means we have to use a lot less weights and biases.
Thanks @Joel for pointing out that it is sufficient to make all numbers positive in the first step and reversing it in the last one, which makes -8 weights. Thanks @xnor for pointing out an even shorter max/min method which makes -22 weights! Thanks @DustinG.Mixon for the tip of combining certain matrices which result in another -4 weights!
function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end
Try it online!
$endgroup$
Octave, 96 88 87 84 76 54 50 weights & biases
This 6-layer neural net is essentially a 3-step sorting network built from a very simple min/max network as a component. It is basically the example network from wikipedia as shown below, with a small modification: The first two comparisons are done in parallel. To bypass negative numbers though the ReLU, we just add 100 first, and then subtract 100 again at the end.

So this should just be considered as a baseline as it is a naive implementation. It does however sort all possible numbers that do not have a too large magnitude perfectly. (We can adjust the range by replacing 100 with another number.)
Try it online!
max/min-component
There is a (considerably less elegant way more elegant now, thanks @xnor!) way to find the minimum and maximum of two numbers using less parameters:
$$beginalign min &= a - ReLU(a-b) \ max &= b + ReLU(a-b) endalign$$
This means we have to use a lot less weights and biases.
Thanks @Joel for pointing out that it is sufficient to make all numbers positive in the first step and reversing it in the last one, which makes -8 weights. Thanks @xnor for pointing out an even shorter max/min method which makes -22 weights! Thanks @DustinG.Mixon for the tip of combining certain matrices which result in another -4 weights!
function z = net(u)
a1 = [100;100;0;100;100;0];
A1 = [1 0 0 0;0 0 1 0;1 0 -1 0;0 1 0 0;0 0 0 1;0 1 0 -1];
B1 = [1 0 -1 0 0 0;0 0 0 1 0 -1;0 1 1 0 0 0;0 0 0 0 1 1];
A2 = [1 0 0 0;0 1 0 0;1 -1 0 0;0 0 1 0;0 0 0 1;0 0 1 -1];
A3 = [1 0 -1 0 0 0;0 1 1 0 0 0;0 0 0 1 0 -1;0 1 1 -1 0 1;0 0 0 0 1 1];
B3 = [1 0 0 0 0;0 1 0 -1 0;0 0 1 1 0;0 0 0 0 1];
b3 = -[100;100;100;100];
relu = @(x)x .* (x>0);
id = @(x)x;
v = relu(A1 * u + a1);
w = id(B1 * v) ;
x = relu(A2 * w);
y = relu(A3 * x);
z = id(B3 * y + b3);
% disp(nnz(a1)+nnz(A1)+nnz(B1)+nnz(A2)+nnz(A3)+nnz(B3)+nnz(b3)); %uncomment to count the total number of weights
end
Try it online!
edited Sep 30 at 11:57
answered Sep 27 at 14:29
flawrflawr
39.6k7 gold badges84 silver badges221 bronze badges
39.6k7 gold badges84 silver badges221 bronze badges
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
$begingroup$
Might you get a shorter min-max gadget with(a - relu(a-b), b + relu(a-b))?
$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
|
show 2 more comments
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
$begingroup$
Might you get a shorter min-max gadget with(a - relu(a-b), b + relu(a-b))?
$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
1
1
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
$begingroup$
The constant offsets are basically used to make the inputs non-negative. Once done in the first layer, all intermediate outputs of the comparison blocks are non-negative and it suffices to change it back only in the last layer.
$endgroup$
– Joel
Sep 27 at 23:47
1
1
$begingroup$
Might you get a shorter min-max gadget with
(a - relu(a-b), b + relu(a-b))?$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
Might you get a shorter min-max gadget with
(a - relu(a-b), b + relu(a-b))?$endgroup$
– xnor
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@joel Oh now I see, that makes a lot of sense:)
$endgroup$
– flawr
Sep 28 at 0:00
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
$begingroup$
@xnor Thanks a lot that makes a huge difference!!!!
$endgroup$
– flawr
Sep 28 at 0:16
1
1
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
$begingroup$
Inconsequential nitpick: The score for the first bias is nnz(A1*a0), not nnz(a0). (Or else we must pay the price of an identity matrix.) These numbers are the same in this case.
$endgroup$
– Dustin G. Mixon
Sep 28 at 12:12
|
show 2 more comments
If this is an answer to a challenge…
…Be sure to follow the challenge specification. However, please refrain from exploiting obvious loopholes. Answers abusing any of the standard loopholes are considered invalid. If you think a specification is unclear or underspecified, comment on the question instead.
…Try to optimize your score. For instance, answers to code-golf challenges should attempt to be as short as possible. You can always include a readable version of the code in addition to the competitive one.
Explanations of your answer make it more interesting to read and are very much encouraged.…Include a short header which indicates the language(s) of your code and its score, as defined by the challenge.
More generally…
…Please make sure to answer the question and provide sufficient detail.
…Avoid asking for help, clarification or responding to other answers (use comments instead).
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fcodegolf.stackexchange.com%2fquestions%2f193624%2fsort-with-a-neural-network%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
2
$begingroup$
@Close-voter: What exactly is unclear? I don't think either of the previous NN challenges was so well specified.
$endgroup$
– flawr
Sep 27 at 14:44
1
$begingroup$
No - skip connections are not allowed.
$endgroup$
– Dustin G. Mixon
Sep 27 at 16:13
1
$begingroup$
@DustinG.Mixon I actually just found an approach for the max/min that only uses 15 weights instead of 16, but it is considerably less elegant:)
$endgroup$
– flawr
Sep 27 at 23:27
3
$begingroup$
This is a nicely specified challenge that I think could serve as a model for future neural-network challenges.
$endgroup$
– xnor
Sep 27 at 23:30
1
$begingroup$
I personally find it difficult to optimize without skipping connections. This is because a sorting NN is required to output numbers close enough to the inputs. So it seems necessary to 'remember' / 'reconstruct' the inputs across layers. I do not see how that could be done easily once $e^t$ is involved since there are no inverses of those functions allowed as activations. So we are only left with the ReLUs for which the baseline (with minor improvements as shown in flawr's answer) is already near optimal.
$endgroup$
– Joel
Sep 28 at 0:16